Matematika kelas 9 tentang parabola
Grafik Persamaan Fungsi Kuadrat / Parabola
A. Bentuk Umum dan Sifat Parabola
Kurva fungsi kuadrat y = f( x ) = ax2 + bx + c, a tidak sama dengan nol ( 0 ) berbentuk parabola.
Jika nilai a (+) maka parabola terbuka ke atas dan mempunyai nilai ekstrem minimum
Jika nilai a ( - ) maka parabola terbuka ke bawah dan mempunyai nilai ekstrem maksimum
Koordinat titik puncak / titik ekstrem / titik stationer / titik balik parabola adalah ( Xp , Yp )
dengan :
Xp = absis ( x ) titik puncak = sumbu simetri = absis ( x ) saat mencapai nilai maksimum/minimum
Yp = ordinat ( y ) titik puncak = nilai ekstrem/nilai stationer/nilai maksimum/nilai minimum
B. Sketsa Grafik Fungsi Kuadrat / Parabola
Langkah-langkah dalam membuat sketsa grafik fungsi kuadrat/parabola ( y = ax2 + bx + c ) :
1. menentukan titik potong grafik dengan sumbu x → y = 0
kemudian difaktorkan sehingga diperoleh akar-akarnya yaitu x1 dan x2 . jika kesusahan dalam memfaktorkan coba di cek dulu nilai D nya....
jika D < 0 maka fungsi tersebut memang tidak mempunyai akar-akar persamaan fungsi kuadrat sehingga sketsa grafik fungsi kuadrat tidak memotong sumbu x
jika D > 0 maka fungsi tersebut mempunyai akar-akar persamaan fungsi kuadrat namun kita kesulitan dalam menentukannya... bisa jadi karena angkanya yang susah difaktorkan atau faktornya dalam bentuk desimal. Akar-akarnya dapat kita cari dengan rumus abc :
setelah kita mendapatkan nilai x1 dan x2maka titik potong grafik fungsi kuadrat dengan sumbu x :
( x1 , 0 ) dan ( x2 , 0 )
2. menentukan titik potong grafik dengan sumbu y → x = 0karena x = 0 maka y = cdan titik potong dengan sumbu y = ( 0 , c )
3. menentukan sumbu simetri ( xp ) dan titik ekstrem ( yp )
Posisi grafik fungsi kuadrat/parabola terhadap sumbu x
mengulang pembahasan mengenai titik potong sumbu x → y = 0 ada 3 kemungkinan :
D > 0 → grafik fungsi kuadrat memotong sumbu x di dua titik
D = 0 → grafik fungsi kuadrat menyinggung sumbu x di satu titik
D < 0 → grafik fungsi kuadrat tidak memotong sumbu x
dengan menggabungkan dengan nilai a nya dapat dibuat sketsa grafik fungsi kuadrat/parabola :
C. Persamaan Fungsi Kuadrat / Parabola
1. Diketahui tiga titik sembarang
Rumus : y = ax2 + bx + c
nilai a, b dan c ditentukan dengan eliminasi.
2. Parabola memotong sumbu x di dua titik ( x1 , 0 )dan ( x2 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x - x1 ).( x - x2 )
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
3. Parabola menyinggung sumbu x di satu titik ( x1 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x - x1 )2
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
4. Parabola melalui titik puncak ( xp , yp ) dan melalui satu titik sembarang.
Rumus : y = a ( x - xp )2 + yp
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
D. Hubungan Kurva Persamaan Kuadrat / Parabola dan Persamaan Garis Lurus
Kurva fungsi kuadrat y = f( x ) = ax2 + bx + c, a tidak sama dengan nol ( 0 ) berbentuk parabola.
Jika nilai a ( - ) maka parabola terbuka ke bawah dan mempunyai nilai ekstrem maksimum
Koordinat titik puncak / titik ekstrem / titik stationer / titik balik parabola adalah ( Xp , Yp )
dengan :
Xp = absis ( x ) titik puncak = sumbu simetri = absis ( x ) saat mencapai nilai maksimum/minimum
Yp = ordinat ( y ) titik puncak = nilai ekstrem/nilai stationer/nilai maksimum/nilai minimum
B. Sketsa Grafik Fungsi Kuadrat / Parabola
Langkah-langkah dalam membuat sketsa grafik fungsi kuadrat/parabola ( y = ax2 + bx + c ) :
1. menentukan titik potong grafik dengan sumbu x → y = 0
kemudian difaktorkan sehingga diperoleh akar-akarnya yaitu x1 dan x2 . jika kesusahan dalam memfaktorkan coba di cek dulu nilai D nya....
jika D < 0 maka fungsi tersebut memang tidak mempunyai akar-akar persamaan fungsi kuadrat sehingga sketsa grafik fungsi kuadrat tidak memotong sumbu x
jika D > 0 maka fungsi tersebut mempunyai akar-akar persamaan fungsi kuadrat namun kita kesulitan dalam menentukannya... bisa jadi karena angkanya yang susah difaktorkan atau faktornya dalam bentuk desimal. Akar-akarnya dapat kita cari dengan rumus abc :
setelah kita mendapatkan nilai x1 dan x2maka titik potong grafik fungsi kuadrat dengan sumbu x :( x1 , 0 ) dan ( x2 , 0 )
2. menentukan titik potong grafik dengan sumbu y → x = 0karena x = 0 maka y = cdan titik potong dengan sumbu y = ( 0 , c )
3. menentukan sumbu simetri ( xp ) dan titik ekstrem ( yp )
dari penentuan sumbu simetri ( xp ) dan nilai eksterm ( yp ) diperoleh titik puncak grafik fungsi kuadrat/parabola : ( Xp , Yp )
Posisi grafik fungsi kuadrat/parabola terhadap sumbu x
mengulang pembahasan mengenai titik potong sumbu x → y = 0 ada 3 kemungkinan :
D > 0 → grafik fungsi kuadrat memotong sumbu x di dua titik
D = 0 → grafik fungsi kuadrat menyinggung sumbu x di satu titik
D < 0 → grafik fungsi kuadrat tidak memotong sumbu x
dengan menggabungkan dengan nilai a nya dapat dibuat sketsa grafik fungsi kuadrat/parabola :
C. Persamaan Fungsi Kuadrat / Parabola
1. Diketahui tiga titik sembarang
nilai a, b dan c ditentukan dengan eliminasi.
2. Parabola memotong sumbu x di dua titik ( x1 , 0 )dan ( x2 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x - x1 ).( x - x2 )
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
3. Parabola menyinggung sumbu x di satu titik ( x1 , 0 ) dan melalui satu titik sembarang.
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
4. Parabola melalui titik puncak ( xp , yp ) dan melalui satu titik sembarang.
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
D. Hubungan Kurva Persamaan Kuadrat / Parabola dan Persamaan Garis Lurus
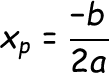
Komentar
Posting Komentar