Persamaan & pertidak samaan kuadrat
1. Batas-batas pertidaksamaan 5x – 7 > 13 adalah...
a. x < -4
b. x > 4
c. x > -4
d. x < 4
e. -4 < x < 4
Pembahasan:
5x – 7 > 13
5x > 20
x > 4
Jawaban: B
2. Semua bilangan positif x yang memenuhi pertidaksamaan √x < 2x jika...
a. x < ¼
b. x < 4
c. x > ¼
d. x > 4
e. x ≤ 4
Pembahasan:

x(1 – 4x) < 0
x = 0 dan x = ¼

Karena x harus bilangan positif, maka nilai x yang memenuhi x > ¼
Jawaban: C
3. Bentuk yang setara (ekuivalen) dengan |4x-5|<13 adalah ...
a. -8 |4x-5| < 13
b. 4x < 18
c. -8 < 4x < 18
d. |15-4x| > -13
e. -12 < 16x < 27
Pembahasan:
|4x-5|<13
-13 + 5 < 4x < 13 + 5
-8 < 4x < 18
Jawaban: C
4. Nilai x yang memenuhi pertidaksamaan ,x∊R adalah...
,x∊R adalah...
a. 1 < x < 2
b. 5 < x < 25
c. x < -1 atau x > 2
d. x < 1 atau x > 2
e. x < 5 atau x > 25
Pembahasan:


(p – 25) (p – 5) = 0
p = 25 dan p = 5
Untuk p = 25, maka nilai x:

x = 2
Untuk p = 5, maka nilai x:

x = 1

HP = {1 < x < 2}
Jawaban: A
5. Himpunan penyelesaian pertidaksamaan adalah...
adalah...
a. {x∣-5 ≤ x ≤ -1}
b. {x∣-1 ≤ x ≤ 5}
c. {x∣-1 < x < 5}
d. {x∣x ≤-1 atau x ≥5}
e {x∣x <-1 atau x >5}
Pembahasan:

(-x + 5) (x + 1) ≤ 0
x ≥ 5 atau x ≤ -1
Jawaban: D
6. Pertidaksamaan , dipenuhi oleh...
, dipenuhi oleh...
a. 0 ≤ x ≤ 1
b. -8 ≤ x < 1
c. -4 < x ≤ 1
d. 1 < x ≤ 7
e. x ≥ -4 dan x < 1
pembahasan:


x = -8 dan x = 1

HP = {-8 ≤ x < 1}
Jawaban: B
7. jika pertidaksamaan mempunyai penyelesaian x > 5 maka nilai a adalah ...
mempunyai penyelesaian x > 5 maka nilai a adalah ...
a. -3/4
b. -3/8
c. 3/8
d. ¼
e. ¾
Pembahasan:

Dari soal diketahui x > 5 kita anggap x = 5, maka kita subtitusikan:

10 – 3a = 7+5a
8a =3
a = 3/8
jawaban: C
8. Agar pertidaksamaan benar, maka nilai x haruslah...
benar, maka nilai x haruslah...
a. x ≤ -2 atau 3 < x ≤ 5
b. -2 ≤ x ≤ 3 atau x ≥ 5
c. x ≤ -2 atau 3 ≤ x ≤ 5
d. 3 < x ≤ 5
e. -2 ≤ x < 3 atau x ≥ 5
Pembahasan:


x = -2, x = 5, dan karena x – 3 adalah penyebut, maka x ≠ 3

jadi, nilai x yang memenuhi adalah:
HP = {-2 ≤ x < 3 atau x ≥ 5}
Jawaban: E
9. Semua nilai x yang memenuhi adalah ...
adalah ...
a. 1/3 < x < 1
b. 1/3 ≤ x < 1
c. x ≤ 1/3 atau x > 1
d. x < 1/3 atau x > 1
e. x < 1/3 atau x ≥ 1
pembahasan:

 merupakan defisit positif, karena D < 0
merupakan defisit positif, karena D < 0
 juga defisit positif
juga defisit positif
Maka:

x = 1/3 dan x = 1
Karena penyebut maka x ≠ 1/3 dan x ≠1

HP = {1/3 < x < 1}
Jawaban: A
10. nilai x yang memenuhi pertidaksamaan |x-2|<5 dan |2x-3|>7 adalah ...
a. -3 < x < 5 atau x > 7
b. x < -3 atau -2 < x < 7
c. -3 < x < -2 atau 5 < x < 7
d. X < -2 atau 5 < x < 7
e. -3 < x < 2 atau x > 5
Pembahasan:
|x-2|<5 maka:
-5 < x – 2 < 5
-5 + 2 < x < 5 + 2
-3 < x < 7
|2x-3|>7 maka:
2x – 3 < -7
2x < -4
x < -2
2x – 3 > 7
2x > 10
x > 5

HP = {-3 < x < -2 atau 5 < x < 7}
Jawaban: C
11. Keliling sebuah persegi panjang adalah 20 m dan luasnya kurang dari 24 m2. Jika panjang salah satu sisinya a meter, maka ...
a. 0 < a < 2 atau a > 12
b. 0 < a < 2√2 atau a > 6√2
c. 0 < a < 3 atau a > 8
d. 0 < a < 2√2 atau a > 4√3
e. 0 < a < 4 atau a > 6
Pembahasan:
Panjang = p
Lebar = a
K = 20 m
2 (p + a) = 20
2p + 2a = 20
2p = 20 – 2a
P = 10 – a
L < 24
P . a < 24
(10 – a) a < 24

a = 4 dan a = 6

Karena ukuran panjang harus bernilai positif, maka nilai a adalah:
HP ={0 < a < 4 atau a > 6 }
Jawaban: E
12. Bentuk |5-5x|<5 setara dengan ...
a. -5 < |5-5x|
b. |x-1|<1
c. 5x – 5 < 5
d. 5x – 5 > -5
e. 0 < 5 – 5x < 5
Pembahasan:
|5-5x| < 5
-5 < 5 – 5x < 5 (bagi dengan 5)
-1 < 1 – x < 1
|1-x|<1 atau
|x-1|<1
Jawaban: B
13. Nilai x yang memenuhi adalah ...
adalah ...
a. -2 ≤ x < -1
b. 0 < x ≤ -1
c. X < 2
d. X ≥ 3
e. X ≥ -1
Pembahasan:
x + 3 harus positif, maka:
x + 3 > 0
x > -3
Nilai 2x + 4 juga harus positif, maka:
2x + 4 > 0
2x > -4
x > -2
x + 3 > 2x + 4
-x > 1
x < -1

HP = {-2 ≤ x ≤ -1}
jawaban: A
14. Himpunan penyelesaian dari pertidaksamaan adalah ...
adalah ...
a. {x∣ -3 ≤ x ≤ -1/2}
b. {x∣ -3 ≤ x < -1/2}
c. {x∣ x ≤-3 atau x ≥-1/2}
d. {x∣ x < -3 atau x > -1/2}
e. {x∣ x ≤ -3 atau x > -1/2}
Pembahasan:


-2x – 6 ≥ 0
-2x ≥ 6
x ≤ -3 berarti x
2x + 1 < 0
x > -1/2

HP = { x ≤ -3 atau x > -1/2}
Jawaban: E
15. Semua nilai x yang memenuhi x|x-2| < x – 2 adalah ...
a. x < -1 atau 1 < x < 2
b. x < -2
c. -2 < x < -1
d. x < -1
e. -2 < x < 1
Pembahasan:
x|x-2| < x – 2
syarat untuk x – 2 ≥ 0
(i) Karena x – 2 ≥ 0 maka x ≥ 2
(ii) Karena x – 2 ≥ 0, maka
x ( x – 2) < x – 2

(x – 1) (x - 2) < 0
1 < x < 2
Yang memenuhi syarat (i) dan (ii) tidak ada, maka
HP = {∅}
Untuk syarat x – 2 < 0,
(iii) Karena x – 2 < 0, maka x < 2
(iv) Karena x – 2 < 0, maka
x ( -x + 2) < x – 2

(x – 2) (x + 1) < 0
x > 2 atau x < -1
Yang memenuhi syarat (iii) dan (iv) adalah x < -1
HP = {-1}
Dari HP 1 dan 2 diperoleh HP = {-1}
Jawaban: D
16. Himpunan penyelesaian pertidaksamaan |(|x|+x)| ≤ 2 adalah ...
a. {x∣ 0 ≤ x ≤ 1}
b. {x∣ x ≤ 1}
c. {x∣ x ≤ 3}
d. {x∣ x ≤ 4}
e. {x∣ x ≥ 0}
Pembahasan:
Berdasarkan definisi harga mutlak maka:
Bila x ≤ 0 maka |x|=-x
|-x+x| ≤2
0 ≤ 2
Hal ini berarti dipenuhi oleh semua, x ≤ 0 ... (i)
Bila x ≥ 0, maka |x|=x
|(|x|+x)| ≤ 2
|x+x| ≤ 2
|x| ≤ 1
Maka 0 ≤ x ≤ 1 ...(ii)
Dari (i) dan (ii) diperoleh x ≤ 1
Jawaban: B
17. Penyelesaian dari pertidaksamaan adalah ...
adalah ...
a. -1 ≤ x ≤ 4
b. 2/5 < x ≤ 4 atau x ≤ -1
c. -1 ≤ x < 2/5 atau x ≥ 4
d. 2/5 < x ≤ 4 atau x ≥ 4
e. -1 ≤ x ≤ 2/5 atau x ≥ 4
Pembahasan:

Sehingga diperoleh batas-batas:
x ≥ 4
x ≥ -1
x < 2/5

HP = { -1 ≤ x < 2/5 atau x ≥ 4}
Jawaban: C
18. Fungsi f dengan rumus terdefinisikan pada himpunan ...
terdefinisikan pada himpunan ...
a. {x∣ x ≥ -1}
b. {x∣ x ≥ 0}
c. {x∣ x ≥ 1}
d. {x∣-1 ≤ x ≤ 0 atau x ≥ -1}
e. {x∣ -1 < x ≤ 0 atau x ≥ 1}
Pembahasan:
Syarat agar terdefinisikan adalah:
terdefinisikan adalah:

Batas-batas nilai x adalah x = -1, x= 0, x = 1

HP = { -1 < x ≤ 0 atau x ≥ 1}
Jawaban: E
19. Himpunan penyelesaian pertidaksamaan adalah ...
adalah ...
a. {x∣ -2 ≤ x ≤ 3}
b. {x∣ -3 ≤ x ≤ 2}
c. {x∣ -2 ≤ x ≤ 2}
d. {x∣ -3 ≤ x ≤ 3}
e. {x∣ 0 ≤ x ≤ 3}
Pembahasan:
Bila x ≤ 0, maka |x|=-x, jadi:


(x – 2) (x + 3) ≤ 0
Diperoleh: -3 ≤ x ≤ 2
Karena x < 0, maka: -3 ≤ x ≤ 0
Bila x ≥ 0, maka |x| = x jadi:


(x – 3) (x + 2) ≤ 0
Diperoleh -2 ≤ x ≤ 3
Karena x ≥ 0, maka 0 ≤ x ≤ 3
Dari kedua syarat di atas, didapatkan penyelesaian: -3 ≤ x ≤ 3
Jawaban: D
20. Himpunan penyelesaian dari pertidaksamaan adalah ...
adalah ...
a. {x∈R∣-1<x≤1 atau x≥2}
b. {x∈R∣-2<x<-1 atau x≥2}
c. {x∈R∣-2<x<-1 atau-1≤x<1}
d. {x∈R∣-2≤x<-1 atau-1≤x<1 atau x≥2}
e. {x∈R∣x<-1 atau-1<x≤1 atau x≥2}
Pembahasan:
Bila x ≤ 0, maka |x|=-x, jadi:


Maka diperoleh batas-batas: x = -2 dan x = -1
Bila x ≥ 0, maka |x|=x jadi:


Maka diperoleh batas-batas: x = 2 ; x = 1; x = -1
Daerah penyelesaiannya:

HP = { -1 < x ≤ 1 atau x ≥ 2}
Jawaban: A
21. Nilai-nilai x yang memenuhi: adalah ...
adalah ...
a. -2 < x < 9
b. -3 < x < 9
c. x > 9 atau x < -1
d. x > 9 atau x < -2
e. x > 9 atau x < -3
Pembahasan:

Misalkan |x-3|=p, maka nilai p selalu positif, maka:

(p – 6) (p + 2) > 0
Karena p selalu positif, maka p + 2 > 0, untuk setiap x real, maka:
P – 6 > 0
|x-3|-6>0
(x – 3 + 6) ( x – 3 – 6) > 0
(x + 3) (x – 9) > 0
Diperoleh batas x = -3 dan x = 9 sehingga harga x yang memenuhi adalah x < -3 atau x > 9
Jawaban : E
22. Nilai x yang memenuhi adalah ...
adalah ...
a. 4 < x < 8
b. 2 < x < 5/2
c. 5/2 < x < 4
d. 2 < x < 4
e. -2 < x < 2
Pembahasan:


Diperoleh batas-batas pembuat nolnya yaitu: x = 5/2; x = 2 ; x = 4
Daerah hasilnya:

HP = {2 < x < 4}
Jawaban: D
23. Agar untuk setiap x real maka haruslah ...
untuk setiap x real maka haruslah ...
a. m < 0 atau m > 5
b. -1/3 < m < 5
c. 0 < m < 5
d. 0 ≤ m < 5
e. m < -1/3 atau m > 3
Pembahasan:

Untuk setiap x real, maka D < 0

4m (m – 5) < 0
m = 0 dan m = 5
daerah hasilnya:

HP = { 0 < x < 5}
Jawaban: C
24. Nilai-nilai x yang memenuhi | x + 3 | ≤ | 2x | adalah ...
a. x ≤ -1 atau x ≥3
b. x ≤ -1 atau x ≥1
c. x ≤ -3 atau x ≥ -1
d. x ≤ 1 atau x ≥ 3
e. x ≤ -3 atau x ≥ 1
Pembahasan:
| x + 3 | ≤ | 2x |
((x + 3 ) + (2x))(x + 3) – (2x) ≤ 0
(3x + 3) (-x + 3) ≤ 0
x = -1 dan x = 3
daerah hasilnya adalah:
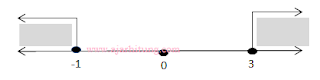
HP = { x ≤ -1 atau x ≥ 3}
Jawaban: A
25. Diketahui Jikq p = xy maka batas-batas nilai p adalah ...
Jikq p = xy maka batas-batas nilai p adalah ...
a. -15 < p < 10
b. 3 < p < 10
c. -10 < p < 15
d. -10 < p < 3
e. 10 < p < 15
Pembahasan:

(x + 5) (x – 1) < 0
Diperoleh: -5 < x < 1

(y + 2) (y – 3) < 0
Diperoleh: -2 < y < 3
P = xy
Batas atas p = -5 . (-2) = 10
Batas bawah p = -5 . 3 = -15
Jadi, batas-batas nilai p adalah: -15 < p < 10
Jawaban: A
a. x < -4
b. x > 4
c. x > -4
d. x < 4
e. -4 < x < 4
Pembahasan:
5x – 7 > 13
5x > 20
x > 4
Jawaban: B
2. Semua bilangan positif x yang memenuhi pertidaksamaan √x < 2x jika...
a. x < ¼
b. x < 4
c. x > ¼
d. x > 4
e. x ≤ 4
Pembahasan:

x(1 – 4x) < 0
x = 0 dan x = ¼

Karena x harus bilangan positif, maka nilai x yang memenuhi x > ¼
Jawaban: C
3. Bentuk yang setara (ekuivalen) dengan |4x-5|<13 adalah ...
a. -8 |4x-5| < 13
b. 4x < 18
c. -8 < 4x < 18
d. |15-4x| > -13
e. -12 < 16x < 27
Pembahasan:
|4x-5|<13
-13 + 5 < 4x < 13 + 5
-8 < 4x < 18
Jawaban: C
4. Nilai x yang memenuhi pertidaksamaan
 ,x∊R adalah...
,x∊R adalah...a. 1 < x < 2
b. 5 < x < 25
c. x < -1 atau x > 2
d. x < 1 atau x > 2
e. x < 5 atau x > 25
Pembahasan:


(p – 25) (p – 5) = 0
p = 25 dan p = 5
Untuk p = 25, maka nilai x:

x = 2
Untuk p = 5, maka nilai x:

x = 1

HP = {1 < x < 2}
Jawaban: A
5. Himpunan penyelesaian pertidaksamaan
 adalah...
adalah...a. {x∣-5 ≤ x ≤ -1}
b. {x∣-1 ≤ x ≤ 5}
c. {x∣-1 < x < 5}
d. {x∣x ≤-1 atau x ≥5}
e {x∣x <-1 atau x >5}
Pembahasan:

(-x + 5) (x + 1) ≤ 0
x ≥ 5 atau x ≤ -1
Jawaban: D
6. Pertidaksamaan
 , dipenuhi oleh...
, dipenuhi oleh...a. 0 ≤ x ≤ 1
b. -8 ≤ x < 1
c. -4 < x ≤ 1
d. 1 < x ≤ 7
e. x ≥ -4 dan x < 1
pembahasan:


x = -8 dan x = 1

HP = {-8 ≤ x < 1}
Jawaban: B
7. jika pertidaksamaan
 mempunyai penyelesaian x > 5 maka nilai a adalah ...
mempunyai penyelesaian x > 5 maka nilai a adalah ...a. -3/4
b. -3/8
c. 3/8
d. ¼
e. ¾
Pembahasan:

Dari soal diketahui x > 5 kita anggap x = 5, maka kita subtitusikan:

10 – 3a = 7+5a
8a =3
a = 3/8
jawaban: C
8. Agar pertidaksamaan
 benar, maka nilai x haruslah...
benar, maka nilai x haruslah...a. x ≤ -2 atau 3 < x ≤ 5
b. -2 ≤ x ≤ 3 atau x ≥ 5
c. x ≤ -2 atau 3 ≤ x ≤ 5
d. 3 < x ≤ 5
e. -2 ≤ x < 3 atau x ≥ 5
Pembahasan:


x = -2, x = 5, dan karena x – 3 adalah penyebut, maka x ≠ 3

jadi, nilai x yang memenuhi adalah:
HP = {-2 ≤ x < 3 atau x ≥ 5}
Jawaban: E
9. Semua nilai x yang memenuhi
 adalah ...
adalah ...a. 1/3 < x < 1
b. 1/3 ≤ x < 1
c. x ≤ 1/3 atau x > 1
d. x < 1/3 atau x > 1
e. x < 1/3 atau x ≥ 1
pembahasan:

 merupakan defisit positif, karena D < 0
merupakan defisit positif, karena D < 0 juga defisit positif
juga defisit positifMaka:

x = 1/3 dan x = 1
Karena penyebut maka x ≠ 1/3 dan x ≠1

HP = {1/3 < x < 1}
Jawaban: A
10. nilai x yang memenuhi pertidaksamaan |x-2|<5 dan |2x-3|>7 adalah ...
a. -3 < x < 5 atau x > 7
b. x < -3 atau -2 < x < 7
c. -3 < x < -2 atau 5 < x < 7
d. X < -2 atau 5 < x < 7
e. -3 < x < 2 atau x > 5
Pembahasan:
|x-2|<5 maka:
-5 < x – 2 < 5
-5 + 2 < x < 5 + 2
-3 < x < 7
|2x-3|>7 maka:
2x – 3 < -7
2x < -4
x < -2
2x – 3 > 7
2x > 10
x > 5

HP = {-3 < x < -2 atau 5 < x < 7}
Jawaban: C
11. Keliling sebuah persegi panjang adalah 20 m dan luasnya kurang dari 24 m2. Jika panjang salah satu sisinya a meter, maka ...
a. 0 < a < 2 atau a > 12
b. 0 < a < 2√2 atau a > 6√2
c. 0 < a < 3 atau a > 8
d. 0 < a < 2√2 atau a > 4√3
e. 0 < a < 4 atau a > 6
Pembahasan:
Panjang = p
Lebar = a
K = 20 m
2 (p + a) = 20
2p + 2a = 20
2p = 20 – 2a
P = 10 – a
L < 24
P . a < 24
(10 – a) a < 24

a = 4 dan a = 6

Karena ukuran panjang harus bernilai positif, maka nilai a adalah:
HP ={0 < a < 4 atau a > 6 }
Jawaban: E
12. Bentuk |5-5x|<5 setara dengan ...
a. -5 < |5-5x|
b. |x-1|<1
c. 5x – 5 < 5
d. 5x – 5 > -5
e. 0 < 5 – 5x < 5
Pembahasan:
|5-5x| < 5
-5 < 5 – 5x < 5 (bagi dengan 5)
-1 < 1 – x < 1
|1-x|<1 atau
|x-1|<1
Jawaban: B
13. Nilai x yang memenuhi
 adalah ...
adalah ...a. -2 ≤ x < -1
b. 0 < x ≤ -1
c. X < 2
d. X ≥ 3
e. X ≥ -1
Pembahasan:
x + 3 harus positif, maka:
x + 3 > 0
x > -3
Nilai 2x + 4 juga harus positif, maka:
2x + 4 > 0
2x > -4
x > -2
x + 3 > 2x + 4
-x > 1
x < -1

HP = {-2 ≤ x ≤ -1}
jawaban: A
14. Himpunan penyelesaian dari pertidaksamaan
 adalah ...
adalah ...a. {x∣ -3 ≤ x ≤ -1/2}
b. {x∣ -3 ≤ x < -1/2}
c. {x∣ x ≤-3 atau x ≥-1/2}
d. {x∣ x < -3 atau x > -1/2}
e. {x∣ x ≤ -3 atau x > -1/2}
Pembahasan:


-2x – 6 ≥ 0
-2x ≥ 6
x ≤ -3 berarti x
2x + 1 < 0
x > -1/2

HP = { x ≤ -3 atau x > -1/2}
Jawaban: E
15. Semua nilai x yang memenuhi x|x-2| < x – 2 adalah ...
a. x < -1 atau 1 < x < 2
b. x < -2
c. -2 < x < -1
d. x < -1
e. -2 < x < 1
Pembahasan:
x|x-2| < x – 2
syarat untuk x – 2 ≥ 0
(i) Karena x – 2 ≥ 0 maka x ≥ 2
(ii) Karena x – 2 ≥ 0, maka
x ( x – 2) < x – 2

(x – 1) (x - 2) < 0
1 < x < 2
Yang memenuhi syarat (i) dan (ii) tidak ada, maka
HP = {∅}
Untuk syarat x – 2 < 0,
(iii) Karena x – 2 < 0, maka x < 2
(iv) Karena x – 2 < 0, maka
x ( -x + 2) < x – 2

(x – 2) (x + 1) < 0
x > 2 atau x < -1
Yang memenuhi syarat (iii) dan (iv) adalah x < -1
HP = {-1}
Dari HP 1 dan 2 diperoleh HP = {-1}
Jawaban: D
16. Himpunan penyelesaian pertidaksamaan |(|x|+x)| ≤ 2 adalah ...
a. {x∣ 0 ≤ x ≤ 1}
b. {x∣ x ≤ 1}
c. {x∣ x ≤ 3}
d. {x∣ x ≤ 4}
e. {x∣ x ≥ 0}
Pembahasan:
Berdasarkan definisi harga mutlak maka:
Bila x ≤ 0 maka |x|=-x
|-x+x| ≤2
0 ≤ 2
Hal ini berarti dipenuhi oleh semua, x ≤ 0 ... (i)
Bila x ≥ 0, maka |x|=x
|(|x|+x)| ≤ 2
|x+x| ≤ 2
|x| ≤ 1
Maka 0 ≤ x ≤ 1 ...(ii)
Dari (i) dan (ii) diperoleh x ≤ 1
Jawaban: B
17. Penyelesaian dari pertidaksamaan
 adalah ...
adalah ...a. -1 ≤ x ≤ 4
b. 2/5 < x ≤ 4 atau x ≤ -1
c. -1 ≤ x < 2/5 atau x ≥ 4
d. 2/5 < x ≤ 4 atau x ≥ 4
e. -1 ≤ x ≤ 2/5 atau x ≥ 4
Pembahasan:

Sehingga diperoleh batas-batas:
x ≥ 4
x ≥ -1
x < 2/5

HP = { -1 ≤ x < 2/5 atau x ≥ 4}
Jawaban: C
18. Fungsi f dengan rumus
 terdefinisikan pada himpunan ...
terdefinisikan pada himpunan ...a. {x∣ x ≥ -1}
b. {x∣ x ≥ 0}
c. {x∣ x ≥ 1}
d. {x∣-1 ≤ x ≤ 0 atau x ≥ -1}
e. {x∣ -1 < x ≤ 0 atau x ≥ 1}
Pembahasan:
Syarat agar
 terdefinisikan adalah:
terdefinisikan adalah:
Batas-batas nilai x adalah x = -1, x= 0, x = 1

HP = { -1 < x ≤ 0 atau x ≥ 1}
Jawaban: E
19. Himpunan penyelesaian pertidaksamaan
 adalah ...
adalah ...a. {x∣ -2 ≤ x ≤ 3}
b. {x∣ -3 ≤ x ≤ 2}
c. {x∣ -2 ≤ x ≤ 2}
d. {x∣ -3 ≤ x ≤ 3}
e. {x∣ 0 ≤ x ≤ 3}
Pembahasan:
Bila x ≤ 0, maka |x|=-x, jadi:


(x – 2) (x + 3) ≤ 0
Diperoleh: -3 ≤ x ≤ 2
Karena x < 0, maka: -3 ≤ x ≤ 0
Bila x ≥ 0, maka |x| = x jadi:


(x – 3) (x + 2) ≤ 0
Diperoleh -2 ≤ x ≤ 3
Karena x ≥ 0, maka 0 ≤ x ≤ 3
Dari kedua syarat di atas, didapatkan penyelesaian: -3 ≤ x ≤ 3
Jawaban: D
20. Himpunan penyelesaian dari pertidaksamaan
 adalah ...
adalah ...a. {x∈R∣-1<x≤1 atau x≥2}
b. {x∈R∣-2<x<-1 atau x≥2}
c. {x∈R∣-2<x<-1 atau-1≤x<1}
d. {x∈R∣-2≤x<-1 atau-1≤x<1 atau x≥2}
e. {x∈R∣x<-1 atau-1<x≤1 atau x≥2}
Pembahasan:
Bila x ≤ 0, maka |x|=-x, jadi:


Maka diperoleh batas-batas: x = -2 dan x = -1
Bila x ≥ 0, maka |x|=x jadi:


Maka diperoleh batas-batas: x = 2 ; x = 1; x = -1
Daerah penyelesaiannya:

HP = { -1 < x ≤ 1 atau x ≥ 2}
Jawaban: A
21. Nilai-nilai x yang memenuhi:
 adalah ...
adalah ...a. -2 < x < 9
b. -3 < x < 9
c. x > 9 atau x < -1
d. x > 9 atau x < -2
e. x > 9 atau x < -3
Pembahasan:

Misalkan |x-3|=p, maka nilai p selalu positif, maka:

(p – 6) (p + 2) > 0
Karena p selalu positif, maka p + 2 > 0, untuk setiap x real, maka:
P – 6 > 0
|x-3|-6>0
(x – 3 + 6) ( x – 3 – 6) > 0
(x + 3) (x – 9) > 0
Diperoleh batas x = -3 dan x = 9 sehingga harga x yang memenuhi adalah x < -3 atau x > 9
Jawaban : E
22. Nilai x yang memenuhi
 adalah ...
adalah ...a. 4 < x < 8
b. 2 < x < 5/2
c. 5/2 < x < 4
d. 2 < x < 4
e. -2 < x < 2
Pembahasan:


Diperoleh batas-batas pembuat nolnya yaitu: x = 5/2; x = 2 ; x = 4
Daerah hasilnya:

HP = {2 < x < 4}
Jawaban: D
23. Agar
 untuk setiap x real maka haruslah ...
untuk setiap x real maka haruslah ...a. m < 0 atau m > 5
b. -1/3 < m < 5
c. 0 < m < 5
d. 0 ≤ m < 5
e. m < -1/3 atau m > 3
Pembahasan:

Untuk setiap x real, maka D < 0

4m (m – 5) < 0
m = 0 dan m = 5
daerah hasilnya:

HP = { 0 < x < 5}
Jawaban: C
24. Nilai-nilai x yang memenuhi | x + 3 | ≤ | 2x | adalah ...
a. x ≤ -1 atau x ≥3
b. x ≤ -1 atau x ≥1
c. x ≤ -3 atau x ≥ -1
d. x ≤ 1 atau x ≥ 3
e. x ≤ -3 atau x ≥ 1
Pembahasan:
| x + 3 | ≤ | 2x |
((x + 3 ) + (2x))(x + 3) – (2x) ≤ 0
(3x + 3) (-x + 3) ≤ 0
x = -1 dan x = 3
daerah hasilnya adalah:

HP = { x ≤ -1 atau x ≥ 3}
Jawaban: A
25. Diketahui
 Jikq p = xy maka batas-batas nilai p adalah ...
Jikq p = xy maka batas-batas nilai p adalah ...a. -15 < p < 10
b. 3 < p < 10
c. -10 < p < 15
d. -10 < p < 3
e. 10 < p < 15
Pembahasan:

(x + 5) (x – 1) < 0
Diperoleh: -5 < x < 1

(y + 2) (y – 3) < 0
Diperoleh: -2 < y < 3
P = xy
Batas atas p = -5 . (-2) = 10
Batas bawah p = -5 . 3 = -15
Jadi, batas-batas nilai p adalah: -15 < p < 10
Jawaban: A

Komentar
Posting Komentar