Logaritma kelas X



A. Definisi Logaritma
Logaritma adalah operasi matematika yang merupakan invers (kebalikan) dari eksponen atau pemangkatan.
Atau dengan pengertian lain, bentuk eksponen bila dinyatakan dengan notasi logaritma adalah
bila dinyatakan dengan notasi logaritma adalah  .
.
dengan :
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma.
Sebagai catatan, bahwa penulisan sama artinya dengan
sama artinya dengan  .
.
Atau dengan pengertian lain, bentuk eksponen
dengan :
a = basis atau bilangan pokok
b = hasil atau range logaritma
c = numerus atau domain logaritma.
Sebagai catatan, bahwa penulisan
B. Sifat – sifat Logaritma
Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :
Jika a>0, a ≠ 1, m ≠ 1, b>0 dan c>0, maka berlaku :

Contoh Soal :
1. Diketahui dan
dan 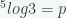 . Nilai
. Nilai  dinyatakan dalam p dan q adalah … (UN SMA 2013)
dinyatakan dalam p dan q adalah … (UN SMA 2013)
1. Diketahui
Penyelesaian :

2. Hasil dari  adalah … (UN SMA 2012)
adalah … (UN SMA 2012)
Penyelesaian :

3. 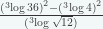 = … (Sipenmaru 1987)
= … (Sipenmaru 1987)
Penyelesaian :
Ingat sifat aljabar

Maka gunakan sifat tersebut untuk menyelesaikan pembilangnya.
Jadi,

Jadi,

Contoh Soal Logaritma dan Pembahasan
Contoh Soal Logaritma 1
Diketahui 3log 5 = x dan 3log 7 = y. maka, nilai dari 3log 245 1/2 adalah … ? (EBTANAS ’98)
Pembahasan 1
3log 245 ½ = 3log (5 x 49) ½
3log 245 ½ = 3log ((5) ½ x (49) ½)
3log 245 ½ = 3log (5) ½ + 3log (72) ½
3log 245 ½ =  ( 3log 5 + 3log 7)
( 3log 5 + 3log 7)
3log 245 ½ =  (x + y)
(x + y)
Jadi, nilai dari 3log 245 1/2 adalah  (x + y).
(x + y).
Contoh Soal Logaritma 2
Jika b = a4, nilai a dan b positif, maka nilai alog b – blog a adalah …? (UMPTN ’97)
Pembahasan 2
Diketahui bahwa b = a4, maka dapat disubstitusi kedalam perhitungan:
alog b – blog a = alog a4 – 
alog b – blog a = 4 (alog a) –  ( alog a)
( alog a)
alog b – blog a = 4 – 
alog b – blog a = 
Jadi, nilai dari alog b – blog a pada soal tersebut adalah  .
.
alog x = n <-> x = an
Pembahasan dari rumus diatas dapat dijabarkan sebagai berikut:
a = bilangan pokok atau basis, a>0 ; a ≠1
x = yang dicari nilai logaritmanya, x>1
n = hasil logaritma
Berdasarkan pernyataan tersebut, sekarang kita mendapatkan bentuk logaritmanya seperti ini:
1. 2x = 5 ↔ x = 2log 5
2. 3y = 8 ↔ y = 3log 8
3, 5z = 3 ↔ z = 5log 3
Ternyata, logaritma ini juga memiliki beberapa sifat diantaranya:
1. Hitunglah nilai – nilai logaritma berikut :
a. 6log 9 + 6log 8 – 6log 2
b. 9log 135 – 9log 5
Jawab :
Berdasarkan sifat logaritma glog (axb) = glog a + glog b dan glog (a:b) = glog a – glog b maka
a. 6log 9 + 6log 8 – 6log 2
= 6log (9.8 /2)
= 6log 36
= 6log 6²
= 2 6log 6 (berdasarkan sifat glog an = n glog a )
=2 . 1
=2
b. 9log 135 – 9log 5
= 9log ( 135 / 5 )
= 9log 27
=3^2log 33
= 3/2 3log 3 ( berdasarkan sifat g^nlog am = m/n glog a )
= 3/2
2. Jika nilai log 3= a dan log 5 = b, tentukan nilai
a. log 75
b. log 1.500
Jawab
Berdasarkan sifat logaritma glog (axb) = glog a + glog b
a. log 75 = log (3 × 5²)
= log 3 + log 5²
= a + 2b
b. log 1500 = log ( 3 × 5 × 100 )
= log 3 + log 5 + log 100
= a + b + log 10²
= a + b + 2
Contoh Soal Logaritma 1
Diketahui 3log 5 = x dan 3log 7 = y. maka, nilai dari 3log 245 1/2 adalah … ? (EBTANAS ’98)
Pembahasan 1
3log 245 ½ = 3log (5 x 49) ½
3log 245 ½ = 3log ((5) ½ x (49) ½)
3log 245 ½ = 3log (5) ½ + 3log (72) ½
3log 245 ½ =  ( 3log 5 + 3log 7)
( 3log 5 + 3log 7)
3log 245 ½ =  (x + y)
(x + y)
Jadi, nilai dari 3log 245 1/2 adalah  (x + y).
(x + y).
Contoh Soal Logaritma 2
Jika b = a4, nilai a dan b positif, maka nilai alog b – blog a adalah …? (UMPTN ’97)
Pembahasan 2
Diketahui bahwa b = a4, maka dapat disubstitusi kedalam perhitungan:
alog b – blog a = alog a4 – 
alog b – blog a = 4 (alog a) –  ( alog a)
( alog a)
alog b – blog a = 4 – 
alog b – blog a = 
Jadi, nilai dari alog b – blog a pada soal tersebut adalah  .
.
Contoh Soal
Sederhanakanlah:
- 2 log 25 – 3 log 5 + log 20
- ½ 2log 82 – 3 2log 3 + 2log 48
Jawab
- 2 log 25 – 3 log 5 + log 20
= log 252 – log 53 + log 20
= log (252/53) + log 20
= log 5 + log 20
= log (5 × 20)
= log 100 = 2
- ½ 2log 82 – 3 2log 3 + 2log 48
= 2log 82½ – 2log 33 + 2log 48
= 2log (9/27) + 2log 48
= 2log 1/3 + 2log 48
= 2log (1/3 × 48)
= 2log 16 = 4














Komentar
Posting Komentar